Ostrosłupy Basiek: Pytanie: czy jest jakieś twierdzenie może... mówiące, że pola figur naprzeciwległych będących ścianami bocznymi ostrosłupa są sobie równe? Oo

Artur z miasta Neptuna: Basiek ... a możesz mi to narysować, bo cholera nie wiem o czym Ty piszesz

Basiek: Sama mam wrażenie, że nie wiem Mogę opisać mój problem, bo narysować... no nie da się chyba

Artur z miasta Neptuna: to opisuj a rysunek ... na kartce + zdjęcie + wrzucasz tutaj linka

Mila: Ściany boczne ostrosłupa są trójkątmi. Trójkąty przystające na pewno mają równe pola − tak jest w ostrosłupach prawidłowych. Inne trójkąty też mogą mieć równe pola i to musisz stwierdzić na podstawie warunków zadania.

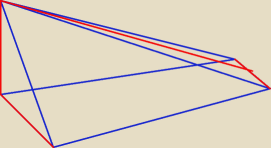
Godzio: Ja rozumiem i powiem, że takowego twierdzenia nie ma Przykład masz narysowany: podstawy są takie same, ale wysokości już nie

Basiek: Więc: Podstawa ostrosłupa jest kwadratem. Jedna z krawędzi bocznych jest prostopadła d podstawy ostrosłupa. Najdłuższa krawędź boczna ma długość 13√2 i jest nachylona do płaszczyzny

	12
podstawy pod kątem α, którego sinus jest równy		. Sporządź rys. i oblicz pole
	13

powierzchni bocznej ostrosłupa. I jako że ta książka ma takie bardziej rozbudowane odpowiedzi.... tu z tyłu jest napisane, że P_b= 2P_ΔACS+2P_ΔABS =.... I to własnie o to mi chodzi, bo nie dodawali wszystkich ścian bocznych... , ale jakby po dwie. No. A co do rysunku, mogę zeskanować; ale z tego to nawet ja mam problem się odczytać Jak wolisz.

Godzio: Nie patrz na odpowiedzi tylko licz, nie jest trudne Z sinusa i 13√2 wyliczysz wysokość (krawędź prostopadła do płaszczyzny podstawy) Z 13√2 masz od razu bok kwadratu, a z tego masz pole dwóch ścian bocznych, ale skoro znasz to to wyliczysz długości innych krawędzi bocznych, a z tu już działa wzór Herona

Basiek: Godzio nie mów mi, błagam, że nie jest trudne. Polecenie brzmi: zróbcie sobie na pojutrze wszystkie zadanka z ostrosłupów z niebieskiej książeczki. Ostatni raz takie dziwy widziałam w gimnazjum i uwierz, nie na tym poziomie. Mam dość Jeszcze 16

Mila: Basiek tam są 2 Δ prostokątne o przyprostokatnych H i a a − bok kwadratu przeciwprostokątna w obydwu =k dwa pozostałe Δ też są prostokątne o bokach a, k i 13√2. Zrób sobie mały model.

Basiek: Jak się przyjrzę rysunkowi dobremu to widzę. Pytanie tylko.... jedna krawędź boczna jest prostopadła do podstawy− wynika z treści, ale druga?

Mila: Co obliczyłaś? Podaj wymiary.

Basiek: a=5 I hm, CS= 12√2 BS=√313 i chyba tylko tyle jest potrzebne.

Basiek: Ech, nie mam sił na takie rzeczy. Przyjdę za jakąś godzinkę i pomożecie mi z jakimiś dwoma zadankami, jeśli będziecie, dobrze? Póki co, dziękuję bardzo. A co do powyższego zadania, wyszło mi na podstawie rys. w odpowiedziach

Mila: czyli masz wszystkie odcinki (13√2)²=338 5²+√313²=338 czyliΔ jest prostokatny na podstawie tw. odwrotnego do tw.PITAGORASA.

Basiek: No tak... odwrotne do Pitagorasa. Nie zdarzyło mi się jeszcze użyć tego twierdzenia, ale faktycznie. Mogę prosić o hm... pomoc w czymś takim: Podstawą ostrosłupa jest trójkąt ostrokątny. Ściany boczne są trójkątami prostokątnymi, których kąty ostre są przy podstawie ostrosłupa. Dwie z krawędzi bocznych mają po 10 cm, a trzecia 20 cm. Oblicz V i pole powierzchni bocznej ostrosłupa. z Pitagorasa (odkrywczo, nie ma co...) obliczyłam krawędzie podstawy: 10√2, 10√5, 10√5 Można jakąś podpowiedź co teraz, albo coś? Bo łagodnie rzecz biorąc utknęłam.

Basiek: Up?

Basiek:

Trivial: Jak to narysować.

Trivial: Źle przeczytałem, zaraz spróbuję znowu.

Basiek: Hm, wcześniej wygooglowałam coś o rogu ściany.... i żeby sobie coś wyobrazić Ale teraz: http://forum.zadania.info/download/file.php?id=2243&sid=9d1dd6f0d441ca69ee8c481ffb464f5c

Godzio: Basiek napisałem wszystko co trzeba zrobić ! Trzeba było iść krok po kroczku, a byś doszła do wyniku

Basiek: Godzio to było wcześniejsze zadanie

Godzio: Aaaa sory

Godzio: Czym jest spodek wysokości w tym ostrosłupie ?

Trivial: Ooo no to teraz już nie będę próbował tego rysować, bo w 3D ciężko.

Basiek: Pewnie środkiem jakiegoś koła. Tylko bo widzisz... ja dostałam 24 zadania do domu. ja nic nie wiem o ostrosłupach tak w ogóle A hm... wikipedii w tym przypadku nie zrozumiałam.

Trivial: Godzio, jak nie wiadomo czym, to wiadomo, że punktem przecięcia się wysokości/(ew. czegoś innego )

Basiek: "Jeśli wszystkie krawędzie ostrosłupa tworzą z podstawą kąty równej miary, to spodek wysokości pokrywa się ze środkiem okręgu opisanego na podstawie (w szczególności − taki okrąg istnieje). Jeśli kąty równej miary tworzą z podstawą ściany boczne, to spodek wysokości pokrywa się ze środkiem okręgu wpisanego w podstawę (w szczególności − taki okrąg istnieje)."

Trivial: symetralnych? Nie pamiętam już tych twierdzonek.

Godzio: http://www.sendspace.pl/file/efd3cf788f90ca42ae75ef7 Masz, robiłem to kilku osobom, to są rzeczy których nie ma w karcie wzorów. Masz tam 2 rzeczy ze stereometrii, które Ci się przydadzą, między innymi to gdzie leży spodek wysokości

Godzio: Trivial ja wiem gdzie jest spodek Baśki pytałem

Trivial: ale ja nie wiem. Który strzał był prawidłowy?

Basiek: "Bądź grzeczny i nie zadawaj głupich pytań!" Wiadomo, że ja nie wiem. A za link− dziękuję

Basiek: "a) Jeśli wszystkie ściany boczne ostrosłupa tworzą z podstawą równe kąty lub jeśli wysokości wszystkich ścian bocznych, poprowadzone z wierzchołka ostrosłupa, są równe, to w podstawę ostrosłupa można wpisać okrąg, a środkiem tego okręgu jest spodek wysokości ostrosłupa. b) Jeśli wszystkie krawędzie boczne ostrosłupa są równe lub jeśli wszystkie krawędzie boczne tworzą z płaszczyzną podstawy równe kąty, to na podstawie ostrosłupa można opisać okrąg, a środkiem tego okręgu jest spodek wysokości ostrosłupa." To by się chyba przydało na pamięć nauczyć, tak?

Trivial:

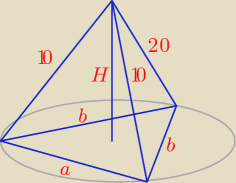
Godzio: a = 10√2 b = 10√5 h − wysokość podstawy (pada na bok a) h² + (5√2)² = (10√5)² ⇒ h = 15√2

	abc
R =		= ...
	2P

H² + R² = 100 ⇒ H = ... I koniec

Godzio: Ty czekaj, przecież krawędzie nie są równe Ale wtopa

Trivial: Nigdy nie przepadałem za tymi zależnościami geometrycznymi... Godziu, dowodzik poproszę, że spodek jest tam gdzie jest, a nie tam gdzie go nie ma.

Basiek: O matko... i córko.... w gruncie rzeczy banalne O.o Ale wiesz co? I tak bym wstawiała na okrąg wpisany, nie opisany

Basiek: <dalej nie widzisz błędu, ale czeka>

Godzio: Ale o spodku nic nie wiemy Trivial chodzi Ci o to co teraz zrobiłem czy to co Basiek napisała (bo jeśli chodzi o teraz to był błąd )

Trivial: Dobra, posiedzę już cicho.

Basiek: Godzio tylko tego nie należy przekombinować. Do tego zad. są jedynie odpowiedzi, co oznacza, że w skali trudności 1−10 ma on 1.

Godzio:

Basiek: http://forum.zadania.info/viewtopic.php?f=21&t=32390 20 stycznia , 12:17 Odp. by się zgadzała Ale co jej tam pada i gdzie, to już nie zrozumiem

Basiek: Dobra, dziękuję, jesteście wielcy Idę lulu